4 Objekte für "sehr große ganze Zahlen"
4.1 Bestandsaufnahme und Projektziele
In den meisten Programmiersprachen werden numerische Daten stets in Formaten fester Größe abgelegt und verarbeitet. So belegt z.B. ein Integer-Wert in Delphi stets 4 Byte. Mit dieser Festlegung sind dann aber auch gleich die Grenzen des Bereichs der "darstellbaren Zahlen" fixiert: wenn wir von den 32 Bit dieser 4 Bytes eines für die Speicherung des Vorzeichens benutzen, dann bleiben 31 Bit für den Betrag der Zahl übrig, was ein "Darstellbarkeitsinterval" von [-231, 231-1], also [-2147483648..2147483647]
ergibt. Die obere Grenze ist dabei um 1 kleiner als vielleicht zunächst erwartet, weil die Null auch noch berücksichtigt werden muss: z.B. kann man in 3 Bit 23 = 8 verschiedene ganze Zahlen speichern, also die Zahlen 0, 1, 2, 3, 4, 5, 6, 7, d.h. alle ganzen Zahlen aus [0, 23-1]!
Wenn man Zahlen außerhalb dieses Bereichs verwenden will, kann man auf Fließkommazahlen ausweichen: der Typ "Single" belegt ebenfalls 4 Byte, speichert aber Werte im Bereich [-3.4 x 1038 .. 3.4 x 1038], allerdings mit reduzierter "Genauigkeit" von etwa 7 bis 8 Dezimalstellen. Diese Fließkommazahlen haben die gelegentlich unangenehme Eigenschaft, zu den Grenzen des Darstellbarkeitsbereichs hin "auszudünnen": Die Zahlen 1.234567 * 1038 und 1.234568 * 1038 liegen um 1*1032 voneinander entfernt, während zwischen 1.234567 und 1.234568 nur die Distanz 0.000001 liegt. Wer eine dichtere Belegung der Zahlengeraden braucht, kann zu den Typen "Double" oder "Extended" übergehen, die aber das Problem nur verschieben, ohne es zu lösen: der Typ "Extended" speichert in je 10 Byte eine Fließkommazahl aus dem Bereich [1.1*104932 .. 1.1 x 104932] mit einer Genauigkeit von etwa 19 bis 20 Dezimalstellen. Mehr ist auf Standard-PCs in Sprachen wie Pascal, C und Java zunächst nicht möglich.
Der prinzipielle Mangel aller Fließkomma-Darstellungen ist, dass zwei hinreichend große benachbarte ganze Zahlen nicht mehr unterscheidbar sind. Das ist für manche Anwendungen (z.B. in der Kryptographie!) nicht tolerierbar. Wenn wir bei den ganzen Zahlen bleiben wollen, gibt es zwar noch den Typ "Int64", der eine ganze Zahl in 8 Byte, also 64 Bit, unterbringt. Damit erhält man zwar den erweiterten Darstellbarkeitsbereich von [-263..263-1], aber auch in diesem Fall hat der Bereich der darstellbaren Zahlen eine harte Grenze.
Wir wollen nun einen eigenen Zahlentyp "TVLInt" (für "Typ Very Long Integer") entwickeln, mit dem wir (fast) beliebig lange ganze Zahlen darstellen und mit ihnen rechnen können. Wir orientieren uns bei unserem Vorgehen daran, wie ganze Zahlen im Dezimalsystem geschrieben werden: dort verwenden wir auch keine feste Stellenzahl, sondern geben immer so viele Stellen, wie die Zahl eben "braucht". Eine passende Datenstruktur, die dieses Vorgehen ermöglicht, haben wir im vorigen Kapitel schon kennengelernt: die Liste! Die Grundidee ist also, eine ganze Zahl durch eine Liste ihrer Stellenwerte darzustellen - nicht gerade originell, aber es führt zum Erfolg.
4.2 Sehr lange Integerzahlen
Was müssen wir nun also implementieren für so eine TVLInt-Zahl? Der Typ TVLInt wird sicher von TObject abgeleitet werden. Außerdem muss eine interne Liste für die Stellen der Zahl vorhanden sein:
type TVLInt = class(TObject)
protected
FDigits : TList;
public
{......}
end;
Der möglicherweise naheliegenden Versuchung, TVLInt gleich von TList abzuleiten, sollte man widerstehen, weil dann automatisch das gesamte Interface von TList in TVLInt veröffentlicht werden würde. Da wir uns jedoch stets um möglichst "kleine" Schnittstellen bemühen wollen, ist es sinnvoller, die Liste als "protected"-Variable zu deklarieren und sie nur intern zu verwenden.
Das allerdings ist auch nicht ganz trivial. Während nämlich eine normale Liste irgendwelche Objekte (also Nachfahren von TObject) speichert, wollen wir hier nur Integerwerte in der Liste ablegen, nämlich die einzelnen Stellen der Zahl. Zunächst werden wir uns auf die dezimale Darstellung beschränken, damit wir es beim Entwickeln etwas leichter haben. Jeder Listenplatz kann also einen der Werte {0, 1, 2, .... 8, 9} enthalten. Um nicht dauernd zu "Typecasts" greifen zu müssen, ist es sinnvoll, für den lesenden und schreibenden Zugriff auf die einzelnen Stellen der Zahl Zugriffsmethoden (SetDigit und GetDigit) zu schreiben. Außerdem brauchen wir natürlich wieder einen Konstruktor und eine Free-Methode, die den Destruktor aufruft. Dem Konstruktor soll auch gleich ein String übergebenen werden, aus dem er die entsprechende Zahl konstruieren und ihre Stellen in die Liste FDigits eintragen soll. Schließlich wird noch eine Ausgabefunktion benötigt, die die aktuelle Zahl als String zurückgibt. Damit erhalten wir also die folgende "Minimal-Deklaration" für den Typ TVLInt:
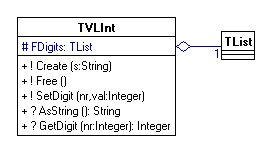
type TVLInt = class(TList)
protected
FDigits : TList
public
constructor Create(s : String);
procedure Free;
procedure SetDigit(nr, val : Integer);
function GetDigit(nr : Integer) : Integer;
function AsString : String;
end;
Der Parameter "nr" in der Deklaration von SetDigit und GetDigit kennzeichnet dabei die Nummer der angesprochenen (Dezimal-)Stelle. Wenn wir der niederwertigsten Stelle die Nummer 0 geben, der nächsten die Nummer 1 usw., dann lässt sich aus der Nummer die Wertigkeit dieser Stelle errechnen: die Stelle mit der Nummer nr hat die Wertigkeit 10nr. Der Eintrag "7" in der 2. Stelle bedeutet also: 7 * 102 = 700.
Aufgabe:
-
Die Minimal-Implementierung: Natürliche Zahlen
Erzeugen Sie ein neues Projekt. Fügen Sie ihm eine neue Unit "mTVLInt" hinzu, in der Sie die obige Deklaration von TVLInt eintragen. Implementieren Sie dann die aufgeführten Methoden. Geben Sie sich besonders bei den Zugriffsmethoden Mühe! Denken Sie hier möglichst alle Fehlermöglichkeiten durch, und versuchen Sie, intelligente Reaktionen zu implementieren.
(Zum Beispiel: Was soll passieren, wenn eine Stelle mit höherer Nummer als die höchste vorhandene gelesen werden soll? Was soll passieren beim Versuch, eine solche Stelle zu schreiben? Wie soll das Objekt auf einen negativen nr-Wert reagieren?)
Bauen Sie im Formular des Programms eine Testumgebung für Ihre TVLInt-Implementierung auf, und testen Sie Ihren Code genau.
Eigentlich könnten wir diese Implementierung so wie sie jetzt ist als Ausgangspunkt für unsere weitere Arbeit an den "Sehr langen Integer-Zahlen" nehmen. Es gibt jedoch eine kleine Delphi-Spezialität, die uns unsere zukünftige Arbeit erheblich vereinfachen kann. Dabei handelt es sich um eine Spracherweiterung, die zwar nicht zur "reinen Lehre der OOP" gehört und daher von Befürwortern eines möglichst sprachen-unabhängigen Informatik-Unterrichts heftig bekämpft wird. (Sie wird daher auch nicht von dem UMLed-Tool unterstützt.) Trotzdem möchte ich dieses Delphi-Sonder-Konstrukt hier benutzen, weil es höchst elegant, enorm effizient und einfach schön ist: die Rede ist von "Properties", also "Eigenschaften". Wir können die Zugriffsfunktionen GetDigit und SetDigit hinter einer "Array-Eigenschaft" unserer TVLInt-Zahl verschwinden lassen, indem wir die Deklaration unserer Klasse wie folgt ergänzen:
type TVLInt = class(TList)
protected
procedure SetDigit(nr, val : Integer);
function GetDigit(nr : Integer) : Integer;
public
constructor Create(s : String);
function AsString : String;
property digit[nr: Integer]: Integer read GetDigit write SetDigit;
end;
Damit steht dem Benutzer eines TVLint-Objekts ein Array namens digit[] zur Verfügung, dessen Felder in Termen und Zuweisungen genau wie die eines "normalen Arrays" benutzt werden können. Haben wir z.B. eine TVLInt-Zahl namens VLI, deren zweite Stelle auf den Wert 7 gesetzt werden soll und deren dritte Stelle wir in eine Integer-Variable a auslesen wollen, dann können wir nun schreiben:
VLI.digit[2] := 7;
a := VLI.digit[3];
Das ist viel übersichtlicher als der direkte Aufruf der eigentlichen Zugriffsmethoden. Intern allerdings setzt der Compiler die Zugriffe auf die Felder von digit[] in entsprechende Aufrufe von GetDigit und SetDigit um - und nimmt uns damit eine Menge Schreibarbeit ab! Dies wird sich besonders bei der Implementierung der verschiedenen Rechenarten auszahlen, weil wir so einen viel leichter lesbaren Quelltext erhalten.
Damit sich die nächste Version unserer TVLInt-Implementierung auch lohnt, wollen wir gleich noch zwei weitere Aufgaben anpacken:
- Wir wollen wir unseren Zahlen ein Vorzeichen spendieren. Üblicherweise wird bei der Standard-Implementierung von Integer-Typen dazu das höchstwertige Bit benutzt, was aber nur dann sinnvoll ist, wenn man mit einem Zahlenformat fester Länge arbeitet. Dies ist bei uns nicht gegeben, so dass wir das Vorzeichen besser in einer bool'schen Variablen ablegen. Wenn wir eine entsprechende Variable FIsNegativ als "protected" deklarieren und eine Zugriffsfunktion IsNegativ implementieren, die den Wert von FIsNegativ zurückliefert, dann hat das Vorzeichen den Charakter einer "Read-Only-Eigenschaft". (Delphi-Profis würden es daher auch wieder als "Property" deklarieren, was hier aber keine wesentlichen Vorteile bringt.)
- Zu den elementaren Operationen, die für alle numerischen Datentypen realisiert sind, gehört die Zuweisung: einer numerischen Variable soll ein neuer Wert zugewiesen werden. Bei Objekten hat sich für eine solche "Daten-Übernahme-Methode" die Bezeichnung Assign eingebürgert. An diese Konvention wollen wir uns auch hier halten: die Prozedur Assign(Source: TVLInt) soll die im aktuellen Zahlobjekt gespeicherte Ziffernliste löschen und danach eine Kopie der in Source gespeicherten TVLInt-Zahl in das aktuelle Zahlobjekt schreiben. Dazu genügt es, das Vorzeichen und (mit Hilfe der neuen Eigenschaft digit[]!) alle Stellen zu kopieren.
Aufgabe:
-
Erste Erweiterungen: Ziffern, Vorzeichen und Zuweisung
Stellen Sie eine Kopie unseres Projekts her und erweitern Sie die TVLInt-Implementierung um die oben beschriebene Eigenschaft digit[] und das Vorzeichen. Vergessen Sie auch nicht, den Konstruktor und die Ausgabefunktion AsString an die neuen Verhältnisse anzupassen!
Kleine Frage am Rande: Wie sollte der Konstruktor reagieren, wenn er den String "-0" übergeben bekommt? Ist das eine negative Zahl?
Fügen Sie dann zunächst eine Auskunftsfunktion DigitCount hinzu, die als Ergebnis die Anzahl der aktuell belegten Dezimalstellen zurückgibt.
Implementieren Sie danach die ebenfalls oben beschriebene Prozedur Assign(Source: TVLInt).
Für die zukünftige Arbeit wird gelegentlich ein Konstruktor CreateCopyOf(Source: TVLInt) recht nützlich sein, der eine Kopie eines schon bestehenden TVLInt-Objekts herstellt. Mit den bisher verfügbaren Methoden sollte Ihnen das ein Leichtes sein!
Ergänzen Sie gegebenenfalls Ihre Testumgebung, und überzeugen Sie sich davon, dass der neue Code korrekt funktioniert.
4.3 Vergleiche von TVLInt-Zahlen
Zu den elementarsten Operationen mit Zahlen gehört der Größenvergleich: von zwei Zahlen ist zu entscheiden, ob Sie gleich sind oder welche der beiden die größere ist. Die Lage wird dadurch verkompliziert, dass wir unseren Zahlen inzwischen schon ein Vorzeichen verpasst haben. Um das Problem in einzelne, leichter lösbare Teilprobleme zu zerlegen, ist es günstig, zunächst einmal die Absolut-Beträge zweier Zahlen zu vergleichen, d.h. das Vorzeichen erst einmal unberücksichtigt zu lassen.
Aufgabe:
-
Test auf Gleichheit
Stellen Sie eine Kopie unseres Projekts her und erweitern Sie die TVLInt-Implementierung um eine als "public" deklarierte Funktion IsEqualTo(CVLI: TVLInt): Boolean, die genau dann TRUE zurückgibt, wenn die aktuelle Zahl mit der übergebenen Vergleichszahl CVLI übereinstimmt.
(Zur Erinnerung: Zwei Zahlen sind genau dann gleich, wenn Sie in allen Stellen übereinstimmen und dasselbe Vorzeichen haben.)
Aus technischen Gründen ist es sinnvoll, für den Vergleich mit "Null" eine eigene Vergleichsfunktion IsNull: Boolean zur Verfügung zu stellen. Implementieren Sie auch diese Funktion.
Passen Sie Ihre Testumgebung geeignet an, und überzeugen Sie sich davon, dass der Test auf Gleichheit in allen Fällen korrekt funktioniert.
-
Vergleich der Absolut-Beträge
Stellen Sie wieder eine Kopie unseres Projekts her und erweitern Sie die TVLInt-Implementierung um eine zunächst als "public" deklarierte Funktion AbsCompareWith(CVLI: TVLInt): Integer, die den Betrag der aktuellen Zahl mit dem Betrag der übergebenen VLInt-Zahl CVLI vergleicht und folgende Ergebnisse zurückgibt:
| Bedingung |
Ergebnis |
| |Aktuelle Zahl| > |CVLI| |
1 |
| |Aktuelle Zahl| = |CVLI| |
0 |
| |Aktuelle Zahl| < |CVLI| |
-1 |
Ändern Sie gegebenenfalls Ihre Testumgebung, und überzeugen Sie sich davon, dass der Vergleich korrekt funktioniert.
-
Vergleich der ganzen Zahlen
Stellen Sie wieder eine Kopie unseres Projekts her. Verbergen Sie dann die Funktion AbsCompareWith im "protected"-Bereich. Fügen Sie nun eine als "public" deklarierte Funktion IsGreaterThan(CVLI: TVLInt): Boolean hinzu, die genau dann TRUE zurückgibt, wenn die aktuelle Zahl größer als die übergebene Vergleichszahl CVLI ist. Eigentlich ist ja "nur noch" das Vorzeichen zu behandeln....
Ergänzen Sie auch eine entsprechende Funktion IsGreaterOrEqualThan()!
Testen Sie Ihre Funktionen zum Größenvergleich!
4.4 Die Grundrechenarten
Nun sollen unsere TVLInt-Zahlen in die Grundschule gehen und das Addieren, Subtrahieren, Multiplizieren und vielleicht sogar das Dividieren lernen. Da TVLInt-Zahlen wie gewöhnliche Dezimalzahlen strukturiert sind, sollten eigentlich alle Algorithmen des schriftlichen Rechnens direkt auf sie übertragen werden können! Wir schauen uns zum Einstieg die Addition zweier positiver Zahlen an:
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| + |
6 |
7 |
8 |
9 |
3 |
1 |
| _ |
1 |
1 |
1 |
_ |
_ |
_ |
| 1 |
9 |
1 |
3 |
4 |
9 |
8 |
Wenn Sie kurz darüber nachdenken, was Sie hier eigentlich tun (wenn Sie's denn überhaupt noch tun - meist überlassen Sie's ja dem TR!), dann sollte Ihnen auch klar werden, wie sie diesen Algorithmus in der TVLInt-Klasse implementieren können. Das einzige Problem dabei ist ein möglicher "Übertrag": wenn die Summe zweier Ziffern größer wird als 9, dann wird in der entsprechenden Stelle des Ergebnisses nur die Einerstelle dieser Ziffernsumme eingetragen, während die Zehnerstelle als "Übertrag" in die nächsthöhere Stelle geschrieben wird. (Übrigens: warum kann der Übertrag beim Addieren zweier Zahlen nie größer werden als 1?)
Ein etwas größeres Problem stellt die Subtraktion zweier positiver Zahlen dar, wobei wir zunächst gutwillig voraussetzen wollen, dass der Minuend einen größeren Betrag hat als der Subtrahend. Schauen wir uns auch hier ein Beispiel an:
| 1 |
8 |
3 |
4 |
5 |
6 |
7 |
| - |
6 |
7 |
8 |
9 |
3 |
1 |
| _ |
1 |
1 |
1 |
_ |
_ |
_ |
| 1 |
1 |
5 |
5 |
6 |
3 |
6 |
Hier taucht ein ähnliches Problem auf wie beim "Übertrag": wenn eine Stelle im Subtrahend größer ist als die entsprechende Stelle im Minuend, dann "geht die Subtraktion nicht". In einer solchen Situation "borgen" wir uns eine 1 von der davorstehenden Stelle: statt "5-9" rechnen wir nun "15-9", und dafür ziehen wir dann in der nächsthöheren Stelle 1 mehr ab als die Stelle im Subtrahenden angibt. Mit diesen Hinweisen sollte Ihnen die Bearbeitung der folgenden Aufgabe nicht mehr all zu schwer fallen.
Aufgaben:
-
Addition natürlicher Zahlen
Stellen Sie eine Kopie unseres Projekts her. Erweitern Sie die TVLInt-Implementierung um eine zunächst als "public" deklarierte Prozedur Funktion AddAbs(S2: TVLInt), die zum Betrag der aktuellen Zahl den Betrag des übergebenen zweiten Summanden S2 hinzuaddiert. Beachten Sie, dass das Ergebnis dabei den ersten Summanden überschreibt!
Passen Sie Ihre Testumgebung geeignet an, und überzeugen Sie sich davon, dass diese "Beträge-Addition" in allen (bisher zugelassenen) Fällen korrekt funktioniert.
-
Subtraktionen natürlicher Zahlen, "die gehen"
Stellen Sie wieder eine Kopie unseres Projekts her. Erweitern Sie die TVLInt-Implementierung um eine zunächst als "public" deklarierte Prozedur SubtrAbs(Sd: TVLInt), die vom eigenen Betrag den Betrag des übergebenen VLInt-Subtrahenden Sd abzieht. Sie dürfen dabei voraussetzen, dass der "eigene" Betrag nicht kleiner ist als der von Sd. Das Ergebnis soll wieder in der aktuellen Zahl stehen; also wird der Minuend überschrieben!
Ein spezielles Problem bei der Subtraktion ist, dass die errechnete Differenz führende Nullen enthalten kann. Schreiben Sie zur Behebung dieses Übels eine interne Prozedur KillLeadingZeros, die alle eventuell vorhandenen führenden Nullen entfernt, und rufen Sie diese am Ende von SubtrAbs auf.
Ergänzen Sie gegebenenfalls Ihre Testumgebung, und überzeugen Sie sich davon, dass diese "Beträge-Subtraktion" (unter den oben gemachten Voraussetzungen) stets korrekt funktioniert.
-
Allgemeine Addition und Subtraktion ganzer Zahlen
Stellen Sie wieder eine Kopie unseres Projekts her. Implementieren Sie dann die allgemeine Addition und Subtraktion für TVLInt-Zahlen, indem Sie ausnützen, was Sie einst in der Unterstufe über das Rechnen mit ganzen Zahlen gelernt haben (sollten):
- Man addiert zwei Zahlen mit gleichem Vorzeichen, indem man ihre Beträge addiert und der Summe das gemeinsame Vorzeichen gibt.
- Man addiert zwei Zahlen mit unterschiedlichem Vorzeichen, indem man vom größeren Betrag den kleineren abzieht und der Differenz das Vorzeichen des betragsgrößeren Summanden gibt.
- Man subtrahiert eine ganze Zahl, indem man ihre Gegenzahl addiert.
Verschieben Sie zunächst die beiden Prozeduren AddAbs und SubtrAbs in den "protected"-Bereich der Klassen-Deklaration. Implementieren Sie dann zwei Prozeduren Add(S2: TVLInt) und Subtr(Su: TVLInt), mit denen die Addition und die Subtraktion "komplett" (d.h. ohne die in den vorigen Aufgaben gemachten Einschränkungen) möglich wird. Dies ist übrigens eine gute Gelegenheit, der Schnittstelle außerdem eine Prozedur ChangeSign hinzuzufügen, welche das Vorzeichen der Zahl umdreht.
Überzeugen Sie sich davon, dass Ihre Zahlen damit die "Strichrechnung" vollständig und korrekt beherrschen.
Na, das ging ja schon ganz gut! Jetzt nur noch schnell die Multiplikation..... Aber leider ist das nicht ganz so einfach. Zwar verursachen die Vorzeichen dabei weniger Aufwand als bei den Strichrechnungen, aber dafür ist die "schriftliche" Multiplikation der Beträge ja eine durchaus nicht-triviale Angelegenheit. In welche elementareren Schritten man eine "schriftliche Multiplikation" zerlegen kann, sollten Sie nun mal in einer eigenen Analyse herausbekommen:
Aufgaben:
-
Forschungen über die Kunst des Multiplizierens
Führen Sie die Multiplikation von 1234 mit 567 schriftlich mit Papier und Bleistift durch. (Ja wirklich, lassen Sie den Taschenrechner weg, er hat jetzt Urlaub!) Ruhen Sie nicht eher als Sie das Ergebnis (699678) erfolgreich erhalten haben. Analysieren Sie dann Ihr Vorgehen genau, und formulieren Sie einen entsprechenden Algorithmus in Worten!
Machen Sie sich klar, welche Operationen bei den einzelnen Schritten benutzt werden. Zumindest zwei der hier benötigten Rechenoperationen sind bisher noch nie aufgetaucht. Die eine ist offensichtlich, aber finden Sie auch die zweite?
-
Erst stellen wir das Werkzeug bereit....
Stellen Sie mal wieder eine Kopie unseres Projekts her. Erweitern Sie die TVLInt-Implementierung um die folgenden Methoden:
- eine Prozedur MultInt(F2: Integer), die die aktuelle Zahl mit der übergebenen Ziffer F2 multipliziert;
- eine Prozedur ShiftLeft(d: Integer), die alle Ziffern der aktuellen Zahl um d Stellen nach links schiebt, also (derzeit!) die Zahl effektiv mit 10d multipliziert.
Überzeugen Sie sich davon, dass diese Hilfsmethoden alles korrekt tun, was wir von ihnen erwarten.
-
....dann lösen wir das Problem!
Stellen Sie wieder eine Kopie unseres Projekts her. Implementieren Sie dann die allgemeine Multipliaktion für TVLInt-Zahlen in einer Prozedur Mult(F2: TVLInt), die die aktuell gespeicherte Zahl mit der in F2 gespeicherten Zahl multipliziert. Beachten Sie auch hier, dass das Ergebnis den ursprünglich gespeicherten ersten Faktor überschreiben soll.
Überzeugen Sie sich davon, dass die Klasse TVLInt damit die Multiplikation vollständig und korrekt beherrscht!
Nun fehlt uns nur noch die Division. Diese stellt allerdings ein besonderes Problem dar, weil die Ganzzahldivision "a durch b" eigentlich zwei Ergebnisse liefert, nämlich a DIV b (was angibt, wie oft b ganz in a enthalten ist) und a MOD b (was angibt, welcher Rest bei diser Division bleibt). Wir lösen das Problem, indem wir diese beiden Operatoren implementieren. Die Frage ist nur: wie?
Aufgaben:
-
Forschungen über die Kunst des Dividierens
Führen Sie die Ganzzahldivision "54321 durch 25" schriftlich mit Papier und Bleistift durch. (Ja wirklich, lassen Sie den Taschenrechner weg, er hat jetzt Urlaub!) Ruhen Sie nicht eher als Sie das Ergebnis ("2172 Rest 21") erfolgreich erhalten haben. Analysieren Sie dann Ihr Vorgehen genau, und formulieren Sie einen entsprechenden Algorithmus in Worten!
-
Erst mal brauchen wir das Ergebnis....
Stellen Sie mal wieder eine Kopie unseres Projekts her. Erweitern Sie die TVLInt-Klasse um eine Methode DivBy(dvsr:TVLInt), die in der aktuellen Zahl a das Ergebnis der Division liefert (also den Wert von [a DIV dvsr]). Sie können sich dazu an dem Algorithmus der schriftlichen Division aus der vorigen Aufgabe orientieren. Es gibt aber auch andere Möglichkeiten.
-
....dann berechnen wir den Rest!
Stellen Sie wieder eine Kopie unseres Projekts her. Implementieren Sie nun die Modulo-Funktion für TVLInt-Zahlen, indem Sie die Prozedur DivBy(dvsr: TVLInt) aus der vorigen Aufgabe als Vorlage für eine neue Methode Modulo(dvsr: TVLInt) nehmen, die nun in der aktuellen Zahl a den Divisionsrest (also der Wert von [a MOD dvsr]) zurückgibt.
Für manche Anwendungssituationen wird man beide Ergebnisse brauchen. Stellen Sie daher zusätzlich eine Methode DivMod(dvsr: TVLInt) zur Verfügung, die in der aktuellen Zahl a den Wert von [a DIV dvsr] und in dvsr den Wert von [a MOD dvsr] zurückliefert.
Überzeugen Sie sich davon, dass die Klasse TVLInt damit die Ganzzahl-Division vollständig und korrekt beherrscht!
4.5 Primzahlsuche
Als erste Anwendung für unsere langen Zahlen wollen wir ein Programm schreiben, das eine Primzahlliste erstellt. Eine natürliche Zahl n ist eine Primzahl, wenn sie genau zwei Teiler hat, nämlich die unvermeidbaren "Trivialteiler" 1 und n selbst. Da es seit Eratosthenes keinen wesentlichen Fortschritt mehr gab bei der Suche nach Algorithmen für die Primzahlbestimmung, bleibt uns kaum etwas anderes übrig, als eine natürliche Zahl nach der anderen durch Probedivisionen auf Teilbarkeit zu untersuchen.
Damit man den Rechner dabei nicht wesentlich mehr arbeiten lässt als nötig, sollte man sich zuvor einige Gedanken über den mathematischen Hintergrund machen, ehe man mit der Programmierung beginnt:
- Als mögliche Prüfteiler für eine natürliche Zahl n lohnen sich nur Primzahlen. (Auf Teilbarkeit durch 15 braucht man nicht mehr zu testen, wenn zuvor schon die Tests auf Teilbarkeit durch 3 und 5 fehlgeschlagen sind!)
- Die 2 ist die einzige gerade Primzahl, aller anderen Primzahlen sind ungerade.
- Es müssen nur solche Primzahlen p als Prüfteiler einer zu untersuchenden Zahl n getestet werden, für die gilt: p^2 <= n. (Wenn es zwischen SQRT(n) und n einen Teiler q von n gibt, dann ist r = n DIV q ebenfalls ein Teiler von n; dieses r liegt dann aber notwendigerweise zwischen 1 und SQRT(n) und muss daher schon vorher gefunden worden sein!)
Also genügt es, die "2" von Hand in unsere Primzahlliste einzutragen und dann alle ungeraden Zahlen beginned mit "3" zu untersuchen. Dabei machen wir sicher noch eine Menge unnötiger Arbeit, weil von drei aufeinanderfolgenden ungeraden Zahlen stets eine durch 3 teilbar ist (und von fünf aufeinanderfolgenden eine durch 5). Entsprechende Optimierungen lassen sich aber später noch problemlos ergänzen, so dass wir nun doch erst mal mit dem Programmieren anfangen wollen.

Aufgabe:
-
Wie gut uns die Zeitung informiert
Das nebenstehende Bild zeigt einen Ausriss aus dem "Offenburger Tageblatt" vom 02. März 2005. Lesen Sie die Meldung aufmerksam durch und beantworten Sie dann folgende Fragen:
- Warum ist die Überschrift Unsinn? Formulieren Sie eine bessere!
- Worin besteht die Leistung des (nun berühmten) Augenarztes?
- Hat die Entdeckung dieser Primzahl einen praktischen Nutzen für die Menschheit?
-
Die erste Anwendung
Schreiben Sie ein Programm, das mit Hilfe der TVLInt-Zahlen systematisch nach Primzahlen sucht. Die gefundenen Primzahlen sollen in einer Listbox ausgegeben werden, immer eine Zahl pro Zeile. Dies hat den zusätzlichen Vorteil, dass die Listbox ihren Inhalt auch leicht in eine Textdatei schreiben kann - und schon haben wir eine transportable Primzahl-Liste in dezimaler Darstellung!
Beachten Sie aber bei der Programmierung des Algorithmus' der Primzahlsuche, dass jede Rechenoperation ihr Ergebnis in derjenigen TVLInt-Zahl zurückliefert, von der aus die entsprechende Rechen-Methode aufgerufen wurde! Dabei darf natürlich keine Information verloren gehen, die Sie später noch brauchen, was eine sorgsame Planung der Berechnung erfordert.
Wenn alles gut funktioniert, dann ergänzen Sie Ihr Primzahl-Such-Programme so, dass es die Zeit misst und ausgibt, die zur Berechnung der ersten 1000 Primzahlen nötig ist. Jetzt wollen wir's nämlich genau wissen!
Ein bißchen langsam ist diese Primzahlsuche ja schon. Auf einem alten Pentium3-Notebook, das mit 550 MHz getaktet ist, braucht die Berechnung der ersten 1000 Primzahlen immerhin fast eine halbe Minute. Vielleicht sollten wir unsere TVLInt-Zahlen nochmals etwas überarbeiten und dabei auf höhere Effizienz achten? Da bietet unser bisheriger Entwurf in der Tat noch eine gute und naheliegende Entwicklungsmöglichkeit:
Bisher haben wir in jeden "Digit" nur eine dezimale Ziffer untergebracht, wir haben also im Dezimalsystem gerechnet. Dies ist nicht die einzige Möglichkeit, die Liste zu nutzen. Wir könnten ja auch im Hex-System rechnen, also mit der Stellenwert-Basis 16, dann würde ein "Digit" schon etwas mehr Informationen tragen, und dieselbe Zahl könnte in weniger TVLInt-Zahlen kodiert werden. Wer aber kann uns hindern, gleich im "Tausender-System" zu rechnen, also mit der Stellenwert-Basis 1000? Die dezimale Zahl 83 726 194 835 würde im "Tausender-System" folgendermaßen dargestellt werden:
83 726 194 835 = 83 * 10003 + 726 * 10002 + 194 * 10001 + 835 * 10000
Sie hätte also dort die 4 Stellen (83), (726), (194) und (835) statt der 11 Dezimalstellen. Eigentlich müssten wir uns nun auch 1000 verschiedene Ziffern ausdenken, um diese Zahl darzustellen.... ;-)
Je mehr Informationen wir in eine Stelle unserer TVLInt-Zahlen hineinpacken, um so weniger Stellen benötigen wir für die Darstellung einer bestimmten Zahl. Welches ist aber nun die größte denkbare Basis für unsere TVLInt-Zahlen? Das vorige Beispiel zeigt, dass es ganz günstig ist, als Stellenwert-Basis eine Zehner-Potenz zu benutzen. Also ist die Frage: welche Zehnerpotenz ist die größte, die man noch in einer Integer-Zahl unterbringen kann? Wie am Anfang dieses Kapitels dargestellt wurde, ist der Bereich, den der Typ Integer abdeckt, durch das Intervall [-2 147 483 648 .... 2 147 483 647] gegeben. Die größte mögliche Stellenwert-Basis ist daher 1 000 000 000 = 109, wir entscheiden uns also für das "Milliarden-System".
Es sind erstaunlich wenig Änderungen an unserer TVLInt-Objekten nötig, wenn wir von dezimaler Kodierung zum "Milliarden-System" übergehen. Natürlich muss der Konstruktor Create() geändert werden, der die Werte der einzelnen Ziffern aus einem übergebenen String errechnet, und analoges gilt für die Ausgabe-Funktion AsString. Darüberhinaus müssen wir überall da, wo bisher in den Rechen-Algorithmen die Zahl 10 in ihrer Eigenschaft als Stellenwert-Basis vorkam, jetzt 1 000 000 000 einsetzen.
Außerdem gibt es noch ein technisches Problem zu lösen. In der Methode MultInt werden zwei "Digits" miteinander multipliziert. Wenn nun (fast) alle Bits eines "Digits" belegt sind, ist das Ergebnis möglicherweise größer, als es ein normaler 32-Bit-Integer verträgt. Zu diesem Zweck gibt es den 64-Bit-Integer namens Int64.
Aufgabe:
-
Wir versuchen zu optimieren....
Stellen Sie eine Kopie Ihres Primzahl-Such-Programms her. Laden Sie das neue Projekt und öffnen Sie die TVLInt-Unit. Ändern Sie die interne Konstante DigitBase von 10 auf 1 000 000 000. Gehen Sie dann kritisch durch die ganze Unit hindurch und suchen Sie nach Stellen, die modifiziert werden müssen. Nehmen Sie die nötigen Änderungen vor.
Beheben Sie dabei auch das oben geschilderte "Int64-Problem". Überprüfen Sie auch die anderen Methoden von TVLInt, ob dieses Problem sonst noch irgend wo auftaucht! Machen Sie sich klar, warum es bei der Addition (und Subtraktion) kein solches Problem gibt!
Testen Sie die neue TVLInt-Bibliothek, indem Sie sie im Primzahl-Such-Programm einsetzen. Vergleichen Sie die erzeugte Primzahlliste mit der in der vorigen Aufgabe erzeugten, um zu testen, ob Ihre neue Bibliothek fehlerfrei arbeitet. Vergleichen Sie auch die Zeit, die nun für die Berechnung der ersten 1000 Primzahlen benötigt wird!
-
....aber geht das wirklich so?
Wir wollen nun die Effizienz unserer beiden TVLInt-Varianten genauer untersuchen. Schreiben Sie dazu einen "Benchmark-Test" für die einzelnen Funktionen der TVLInt-Objekte, in dem Sie die benötigten Zeiten für folgende "Jobs" messen und ausgeben lassen:
- 10000 Additionen
- 1000 Multiplikationen
- 1000 DivBy-Aufrufe
- 1000 DivMod-Aufrufe
- 10000 Create / Free - Zyklen
Benutzen Sie nur wenige, im Programm durch String-Konstanten festgelegte lange Zahlen zum Testen. Schalten Sie in den Compiler-Optionen die "Optimierung" aus, damit das Programm auch wirklich alles tut, was Sie programmiert haben. Je nach der Größe der von Ihnen gewählten Beispielzahlen und der Leistungsfähigkeit Ihres Rechners sind größere oder kleinere Anzahlen von Durchläufen bei den einzelnen Jobs sinnvoller.
Lassen Sie nun die beiden Versionen der TVLInt-Bibliothek zum Wettlauf gegeneinander antreten. Stellen Sie die Ergebnisse Ihrer Untersuchungen übersichtlich dar. Ist das Problem der Effizienz nun vollständig geklärt, oder gibt es noch offene Fragen?




